典型案例

囚徒困境

警察抓到了两名嫌疑犯，为防止两人串供，决定对两个人分别审讯

A/B	B坦白	B抗拒
A坦白	-8,-8	0,-10
A抗拒	-10,0	-1,-1

按上面表格，A和B都坦白，就是纳什均衡点。

A的决策：A会想，我如何才能获得更大收益呢？
如果B坦白了，那么我坦白就会判8年，我抗拒就会判10年，我应该坦白；
如果B抗拒了，我坦白会判0年，我抗拒会判1年，我还是应该坦白。
所以，无论B如何选择，A的最优解都是选择坦白。同样的，无论A如何选择，B的最优解也是坦白。此时，无论是A还是B都没有改变选择的动力，因为一旦改变了，自己的收益就会下降。

然而，两个人都坦白，各判八年，显然不如两个人都抗拒好——这样每个人只会判刑1年。可惜，这个点不是纳什均衡点，任何一方改变了决策，都会让自己的收益提高。每个人按照自己的利益最大化进行选择，不一定是群体利益的最优点。

现实生活对影：开车加塞

智猪博弈

有一个食槽，里面装有十份食物。食槽的开关按钮在另一端，需要按一下按钮食物才能掉下来。现在，有一大一小两只猪，他们都在食槽下眼巴巴的看着，想吃到食物。它们两个既可以自己跑到另一端按按钮然后再回来，也可以等着对方跑去按按钮，自己搭顺风车。只是，跑过去再跑回来需要消耗一定的体力，而且会造成自己后吃食物。

• 每只猪跑去按按钮都要消耗2份食物的体力
• 大猪比小猪吃食物快
• 大猪先吃食物，二者吃食物的比例为9：1
• 小猪先吃食物，二者吃食物的比例为6：4
• 二者同时吃食物，吃食物的比例为7：3

大/小	小猪去	小猪等
大猪去	7-2，3-2	6-2，4
大猪等	9，1-2	0，0

按上面表格，大猪去，小猪的（4，4）就是纳什均衡点。

小猪会思考：
如果大猪去按按钮，我跟着去，获得收益1；我等着，获得收益4，因此我应该等着。
如果大猪不去按按钮，我去按按钮，收益-1；如果我们都等着，我收益为0，因此我还是应该等着。
这样一来，小猪的决策一定是等待。
在小猪等待的情况下，大猪会如何选择呢？如果大猪去按按钮，获得收益4；如果大猪不去按按钮，获得收益0，因此，大猪会选择去按按钮。大猪去按按钮，小猪等待，双方收益为（4，4）的点就是纳什均衡点。

现实生活对影：大公司与小公司

三姬分金

游戏规则是：

• 抽签决定三个人的顺序ABC，按照顺序进行分金币的提议。
• 如果提议未能获得全体人员半数以上（不包括半数）通过，提议人被处死，由下一个人提议。
• 如果提议获得全体人员半数以上通过，按该提议分金币，游戏结束。
• 他们都是聪明的，知道自己的决策会导致什么结果。
• 他们都是理性的，以自己的利益最大化为目标。
• 他们都是邪恶的，在利益最大化的前提下，尽量多杀人。

A提议B和C都反对，杀死A，只剩下B和C，那么C必然会否定B的任何提议，杀死B，C得100

B知道上述结果，从而知道决不能让A死，B就会支持A的任何提议

A知道以上结果，从而提议A100,B0,C0

如果再来一个Z，顺序是Z A B C

Z的提议会是Z98，A0，B1，C1。

Z第一个提议，他会知道以上结果。他知道如果自己死掉，那么A会分走全部的金币，而B和C什么都拿不到。而且，四个人要有超过半数同意自己，至少需要三个人支持，除了自己之外，他还需要拉拢两个人。
显然，拉拢B和C更好。因为如果自己死掉，B和C什么都拿不到，于是只要M给B和C每人一个金币，自己拿98个，B和C就一定支持自己，此时A反对已经没有任何意义了。

现实生活对影：第一大国、第二大国、小国门

胆小鬼博弈

两个人在一条车道上相对着开车，每个人都可以随时打方向盘驶出车道，最先驶出车道的人就会被对方嘲笑为胆小鬼，而一直在车道上狂飙的人获胜,如果两辆车都不驶出车道，最终两辆车就会撞在一起，同归于尽。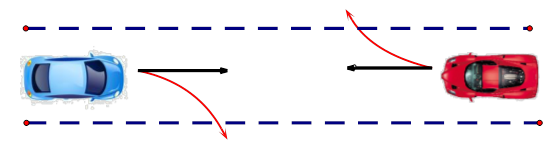

A/B	B示弱	B 死磕
A示弱	2，2	1，3
A死磕	3，1	0，0

如上图，将产生两个纳什均衡点 (1,3) (3,1)

在这个博弈过程中，我们要学会如何伪装死磕到底，但是又在关键时刻变成一个胆小鬼的艺术。毕竟作胆小鬼比作死鬼强得多。

现实生活对影：古巴导弹危机

华容道

赤壁之战后，刘备集团在华容道故意放走曹操也是这个道理。曹操最强大，所以孙权和刘备联合起来进攻曹操。曹操战败之后，如果刘备全力以追击曹操，曹操就可能就命丧于此了。可是，如果这样的话，刘备就要面临和第二强大的孙权对决的局面，这是刘备集团不希望看到的。这时，诸葛亮的智慧就显示出来了，利用义薄云天的关羽守华容道放走曹操，既让曹操活了，孙权集团不敢对自己轻举妄动，也让维护了孙刘联盟，让孙权哑巴吃黄连有苦说不出。虽然这段情节是作者罗贯中的演绎，但是非常合情合理，精彩玄妙，蕴含着深刻的博弈理论。

---